Как оптические дизайнеры оценивают характеристики оптических линз?
- доля
- Время выпуска
- 2022/5/20
Резюме
Хотя графики аберраций полезны для того, чтобы дать оптическому разработчику представление о характеристиках объектива, они обычно являются объективным критерием для пользователя или оценщика объектива. В следующей статье кратко описан метод оптического дизайнера для определения характеристик оптической линзы.

Хотя графики аберраций отлично подходят для предоставления разработчику оптических характеристик характеристик объектива, обычно, особенно для пользователя или оценщика объектива, очень необходим объективный стандарт.
Функция передачи модуляции (MTF) является одним из наиболее широко используемых критериев для оценки изображений в некогерентном свете, где основное внимание уделяется контрасту или резкости изображения.
Фактически, многие современные оптические линзы напрямую измеряются по характеристикам MTF.
Как показано на рисунке 1, рассмотрим оптическую систему, изображающую решетку с синусоидальным распределением интенсивности. При некогерентном освещении интенсивность изображения также синусоидальная, но контраст снижается.
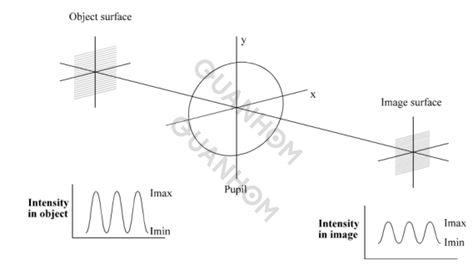
Рис. 1. Сравнение изображений объектов оптической системы.
MTF — контрастность изображения, деленная на контрастность объекта; очевидно, что это функция пространственной частоты, и графики MTF как функции пространственной частоты (обычно в «парах линий/мм») часто используются в оптическом проектировании.
Оптическая передаточная функция определяется как:

Строго говоря, следует различать оптическую передаточную функцию (OTF) и передаточную функцию модуляции (MTF).
OTF — это вектор, который включает в себя фазу и амплитуду изображения, где амплитуда — это MTF.
Фактически, основным фактором при оптическом проектировании является MTF. Фазовый член, иногда называемый фазовой передаточной функцией (PTF), представляет собой отклонение фактического синусоидального изображения от идеального синусоидального изображения, выраженное как функция фазового угла как функция пространственной частоты. Если фаза превышает 180°, MTF может быть отрицательным. Это представляет собой обращение фазы, которое приводит к изменению контрастности изображения. В реальности такое может произойти на высоких частотах многих объективов.
1. Теория
Для систем, освещаемых некогерентным светом, MTF можно получить с помощью преобразования Фурье функции расширения линии. Обычно таким способом получают MTF.
Однако дифракционную ОПФ можно быстро решить с помощью автокорреляционного интегрирования:
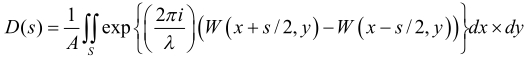
где D(s) = OTF, A = площадь светового зрачка, S — площадь перекрытия двух световых зрачков, W — аберрация волнового фронта, S — упрощенная пространственная частота, равная fλ/NA, а NA — числовая апертура.
2. Геометрическое приближение
В приближении геометрической оптики мы предполагаем, что λ близка к нулю, поэтому MTF (в меридиональном направлении) равна:
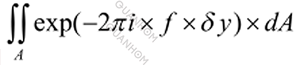
Это интеграция всего ученика, которую на практике можно аппроксимировать простым суммированием.
3. Фактическое решение
Поскольку нам необходимо знать не только сагиттальное направление, но и MTF в меридиональном направлении, MTF в сагиттальном направлении определяется по следующей формуле:
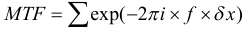
MTF в меридианном направлении получается по следующей формуле:
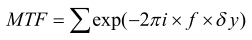
Удобно отслеживать многочисленные (часто более 100) лучи света, но при суммировании учитываются только те лучи, которые действительно проходят через систему. Мы также отслеживаем лучи с разными длинами волн, и при суммировании длины волн могут иметь разный вес. К геометрическому MTF легко добавить поправочный коэффициент, умножив геометрическое MTF на дифракционное MTF идеальной системы. Такой результат позволяет геометрическому MTF быть точным как в системах с большими аберрациями, так и в системах с малыми аберрациями.
Однако при умеренных аберрациях геометрическое MTF обычно дает неутешительные результаты. Теперь нам нужно решить, сколько кольцевых лучей нужно проследить. Взяв лучи так, как показано на рисунке 2, можно увидеть, что площади всех малых площадей в полукруге равны. Легко видеть, что если имеется n колец лучей, то общее число лучей равно 2n. Когда оптическая система симметрична (симметрична относительно плоскости меридиана y), для экономии времени программе не нужно рассчитывать лучи в отрицательном направлении x.
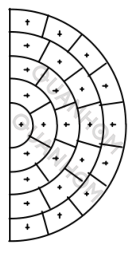
Рисунок 2. Метод построения линий для расчета геометрического MTF
4. Дифракционный предел
При формировании изображения синусоидального объекта линзой с конечной апертурой зрачка предельная частота ее дифракционной МПФ равна:
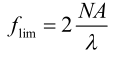
Например, для объектива f/2 с числовой апертурой NA 0,25, когда длина волны λ равна 0,0005 мм, частота среза равна:
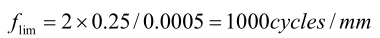
Эта частота соответствует решетке с пространственным периодом 0,001 мм (1 мкм), но обратите внимание, что значение MTF, соответствующее этой частоте, равно нулю. Для 500/циклов мм MTF идеального объектива составляет около 40%, поэтому f/2 — более реалистичная частота.
5. МТФ в ZEMAX
MTF, используемый в ZEMAX, действует как инструмент оценки и как инструмент оптимизации.
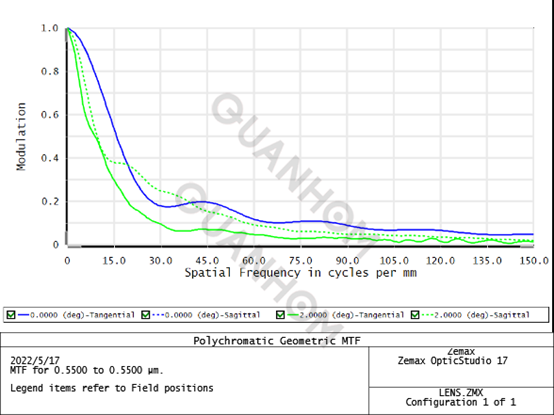
На приведенном выше рисунке всего четыре кривые, две из которых являются меридиональными кривыми MTF, а две другие — сагиттальными кривыми MTF. В поле зрения 0° меридиональная кривая MTF и сагиттальная кривая MTF совпадают; а в поле зрения 2° меридиональная кривая MTF и сагиттальная кривая MTF совершенно разные. Это связано с тем, что PSF становится асимметричной, когда она смещена от оси, что приводит к разнице в ширине и профиле PSF, а также в меридиональном и сагиттальном направлениях. Таким образом, свертка с параксиальным (или геометрическим) изображением приведет к появлению дельты в обоих направлениях. Это также означает, что разрешение в этих двух направлениях разное.
Выше кратко описан метод оценки характеристик оптических линз.
QUANHOM — производитель оптических линз на заказ . Наша команда устраняет разрыв между превосходной производительностью и ограниченным бюджетом, особенно когда мы участвуем в проектах, сочетающих высокую точность. Продукция включает в себя инфракрасные оптические сборки для VIS/SWIR/MWIR/LWIR, окуляры, элементы инфракрасных линз (от моноскопических до инфракрасных линз с быстрым переключением между многопольными и непрерывными инфракрасными линзами) и т. д. Наши опытные и вдохновленные специалисты всегда могут обеспечить оптимизированную ИК-связь. линзовое стекло, и оптико-механический, и оптико-электронный варианты сборки.